Fractality

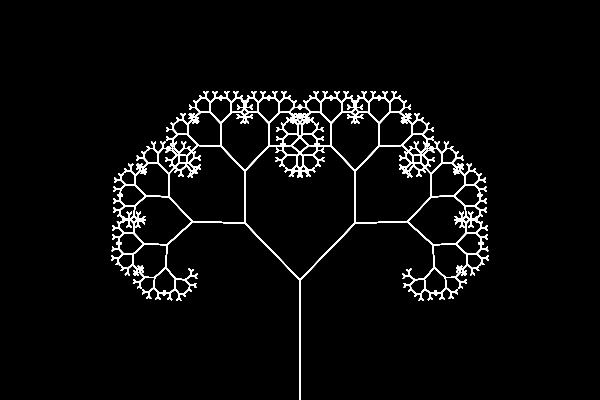
Fractality is the phenomenon of patterns repeating themselves at different scales.

This property is called self-similarity, or when an object as a whole has the same shape as one or more of its parts.

Mathematician Benoit Mandelbrot first discussed this concept in his paper 'How Long Is the Coast of Britain?', where he reflected on the self-similarity of coastlines. He latter coined the term 'fractal' in 1957.

Philosopher and statistician Nassim Nicholas Taleb underlined this property in his book 'The Black Swan' (2007). There, he describes how a short and simple recursive (meaning reapplied to itself) rule can build great complexity. Taleb links this fractal concept to socioeconomic aspects: the size of cities, the distribution of wealth or the returns in financial markets all follow a fractal law. He bases his claim on the idea the fractal has numerical or statistical measures preserved across scales.

This is how the universe unfolds itself: rocks are tiny mountains, branches resemble trees, and ripples mirror greater waves. Swarms of starlings move in unison because each individual makes the same decision at the same time, thus forming a larger coherent entity. Fractality might be seen as a property of our universe.

Fractality is one of my favourite concept. This is because it enables thinking and transferring knowledge at different scales. And my guess is that it can be quite powerful, for example, when applied to problem-solving, decision-making or creativity.

How do we experience fractality in our lives? For example, how do pattern in our behaviour determines some of our small reactions as well as big decisions? What similarities are found in cycles of times, like a day, a year, or a decade? How does the way we treat ourselves affects our relationships to others, as well as our positioning towards society as a whole? These are all areas where fractal thinking can help us see patterns that might have missed before. Other applications of fractality include visual arts, architecture, music, geography, climatology, biology, neurology, or data science.

Where do you perceive fractality around you?

Sources:

• Mandelbrot, B. (1967). How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension. Science, 156(3775), 636–638. https://doi.org/10.1126/science.156.3775.636
• Taleb, N. N. (2007). The Black Swan: The Impact of the Highly Improbable. Random House Publishing Group.

References:

• Fractal. (2023). In Wikipedia. https://en.wikipedia.org/w/index.php?title=Fractal&oldid=1151875042
• Mandelbrot, B. (1992). The Fractal Geometry of Nature. W. H. Freeman and Co.
• Yale University free course on fractal geometry: https://users.math.yale.edu/public_html/People/frame/Fractals/.